こんにちは。keikoです。
今回は「最尤推定」について解説していきます。
ディープラーニングや機械学習は、
統計学と確率なしには語れません。
そして、学び始めた誰もが最初につまずくであろう
最尤推定
について、これからわかりやすく解説していきます。
なお、グラフ等は全てpythonを使っております。
コードについては、
今回はpythonでの実装を解説する目的ではないので、
載せていません。
あらかじめご了承ください。
正規分布
正規分布の確率密度関数は
$$f\left( x\right) =\dfrac{1}{\sqrt{2\pi \sigma ^{2}}}\exp \left( -\dfrac{1}{2}\dfrac{\left( x-\mu \right) ^{2}}{\sigma ^{2}}\right)$$
と表せます。
グラフにすると下のような感じですね。
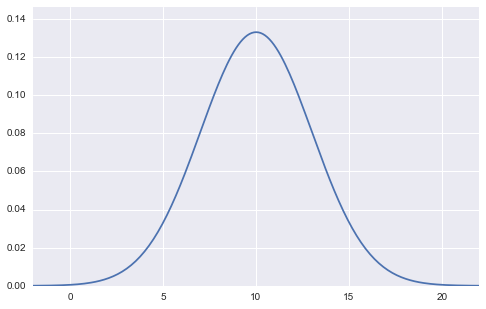
確率密度関数からもわかる通り、
この図は平均μ、標準偏差σの2つのパラメータから成ります。
つまり「μとσがわかれば、正規分布がわかる」ということです。
尤度関数というのは、
「サンプリングしたデータは、もともとどのようなパラメータをもつ確率分布から生まれたものなのか」
というものでした。
ここで、
標本が10個あり、それらが正規分布に従うことはわかっているが、
平均μと標準偏差σがわかっていないものを考えるとしよう。
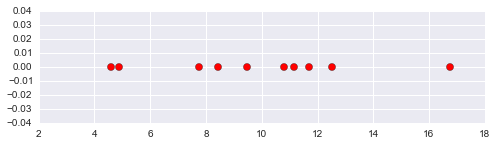
10個の標本が同時に上図の値になった分布を考える。
10個の標本は互いに独立なので、確率密度の積として表せる。
$$P\left(x_{1},x_{2},\ldots x_{10}\right)=P\left(x_{1}\right)P\left(x_{2}\right)\ldots P\left(x_{10}\right)$$
ここで$$P\left( x_{i}\right)$$は全て正規分布に従うので、
$$\begin{aligned}P\left( x_{1},x_{2},\ldots x_{10}\right) =f\left( x_{1}\right) f\left( x_{2}\right) \ldots f\left( x_{10}\right) \end{aligned}$$
と表せる。
これをさらに展開して整理すると、
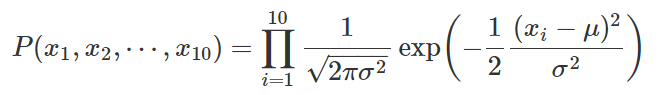
一番最初の確率密度関数の式を使えば書けますね!
これで標本10個の同時確率密度関数ができました。
でも、ここである疑問点が浮かび上がります。
標本は既に実現したものであり、不確定な確率的な値ではないのでは?
そうです。確定値です。
したがって、xは定数と考えられ、μとσが変数だと捉えることができます。
関数は全く同じで、変数をμ、σとしたものを尤度と定義し
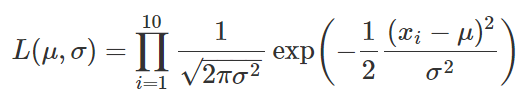
とします。
それではグラフにして見てみましょう。
μ、σが定まっていないので、μ=0,σ=1とします。
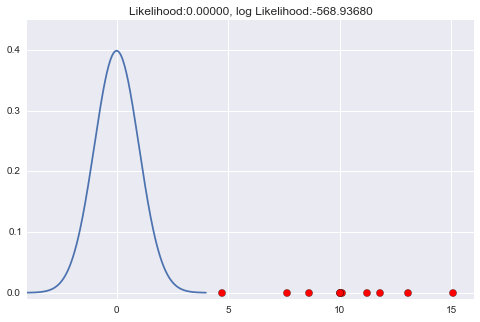
このグラフだと、思いっきり外れているようですね。
この時、尤度の値もかなり小さくなってしまいます。
(尤度というのは、確率(密度)を標本個数分だけ掛けてできたものなので、0~1の値を何度も掛けることになります。したがってかなり小さい数、ほぼゼロになってしまう。
そこで、掛け算を足し算にできる計算のしやすさもあり、対数尤度とすることが多いです。その場合、上記グラフのタイトルの数値もわかりやすい値となります。)
確率密度関数がほとんど0のところばかりが標本となっているので、L(μ,σ)もかなり小さい尤度となりました。
そこで、今度はμ=5、σ=4としてみよう。
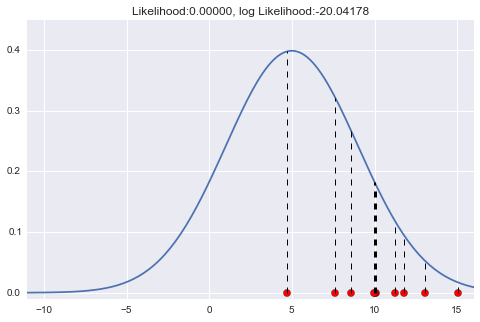
点線で示したところが各標本の尤度に対応します。さっきよりも改善できていますね!
アニメーションで理解を深めよう
それでは、μが変化していくときに尤度がどのように変わっていくのかアニメーションを見てみましょう。
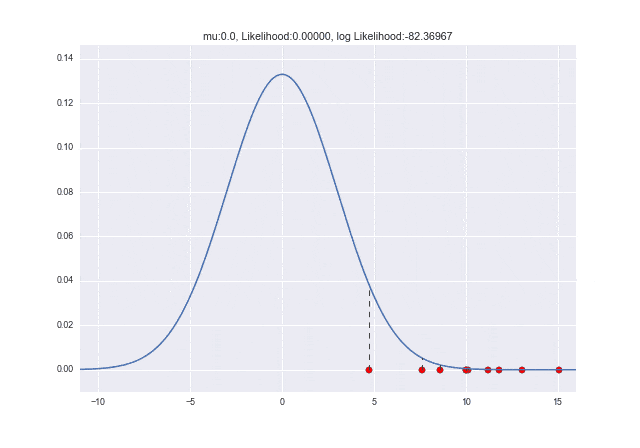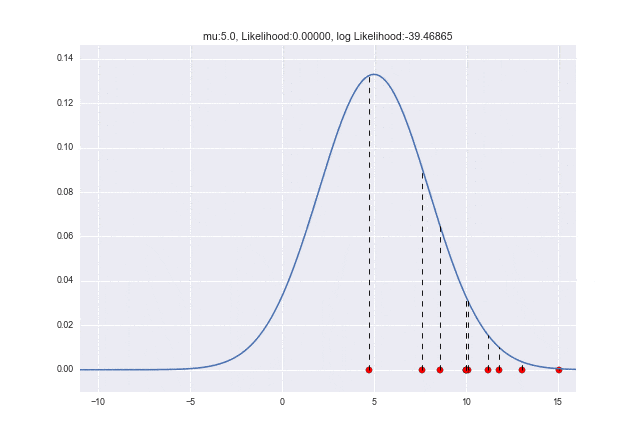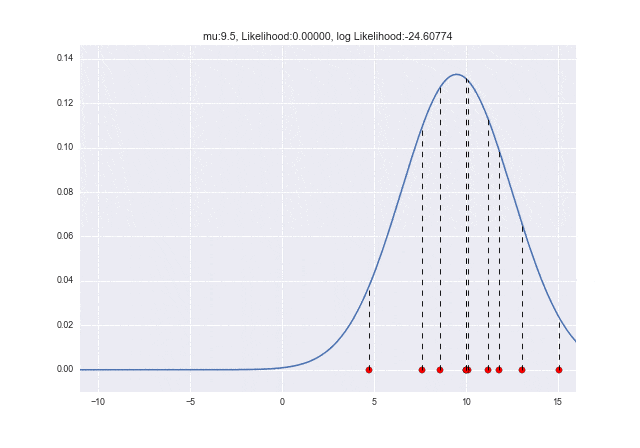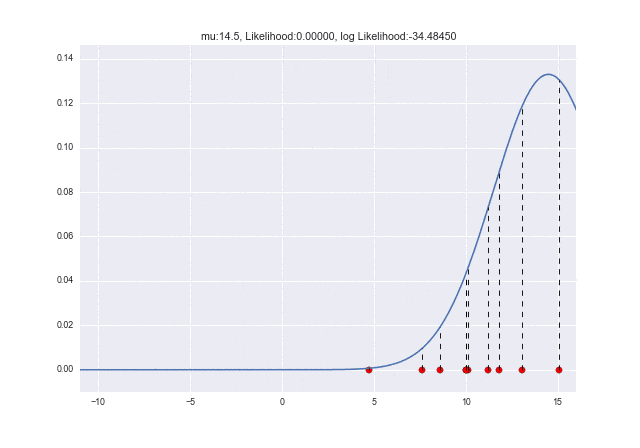
μ=10で対数尤度が最大となっていることがわかります。
では、σが変化していくときにグラフはどのように変化するのでしょうか。
下のアニメーションを見てみよう。
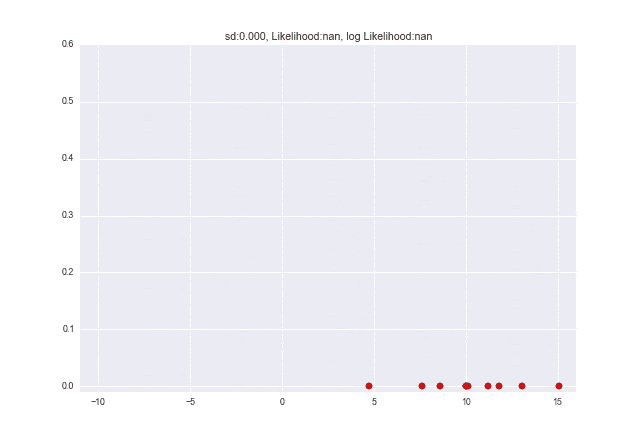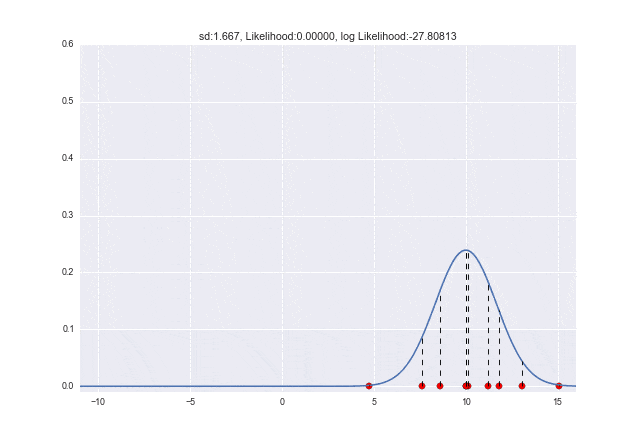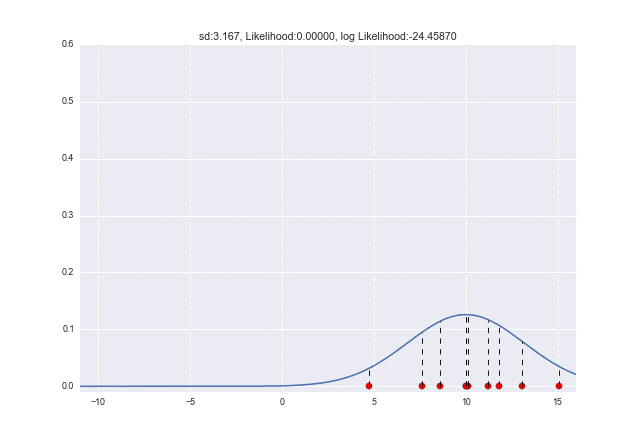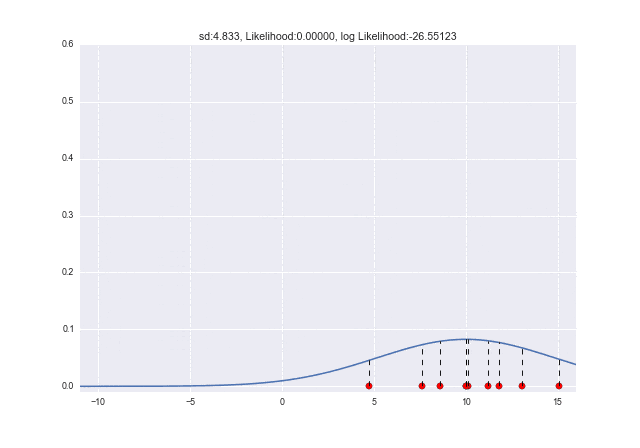
σが変化していくと、σ=2.7ぐらいで対数尤度が最大になっていることがわかります。
(元々10個の標本データを作るときに、σ=3としていたので誤差はありますが、かなり近い値です。)
最尤推定
いよいよ最尤推定について説明します。
下図はσを固定して、μを変化させたときの対数尤度の変化のグラフです。グラフの最大値は尤度をμで微分して0になったときであり、μ=10のときだとわかりますね。
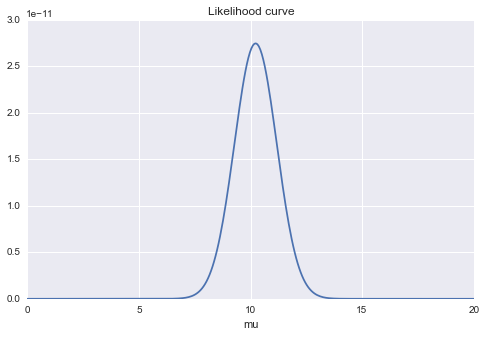
次にμを固定して、σを変化させたときの対数尤度のグラフを見てみます。σ=3あたりに最大値がありそうですね!
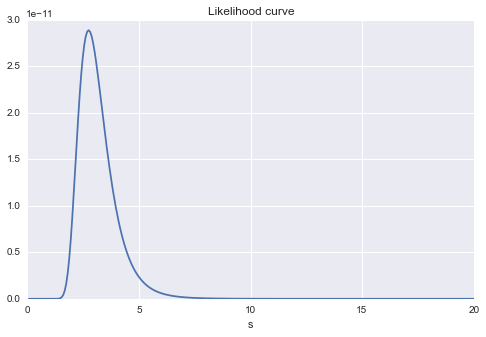
最後にμとσを同時に変数として尤度関数を見てみましょう。
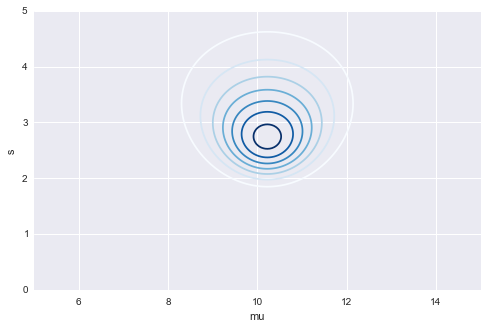
μは10ちょっと多め、σは3ちょっと少なめのところが、最尤推定で得られるμとσの値だとわかります!
以上、最尤推定について解説しました。
おさらいですが、
正規分布は様々なものがあり、μとσの二つの変数で決まる。そこで、自分の持っている標本に一番適した正規分布を探すために、μとσを見つけに行く。これが最尤推定なのだ。
ではでは。



